Energy to Temperature Conversion

This example demonstrates both ConstantCpEnergyModel and CanteraEnergyModel for converting energy deposition to temperature increase in the plasma arc.

============================================================
Energy to Temperature Conversion Models
============================================================

1. Constant Cp Model (Low Fidelity)
------------------------------------------------------------
Energy deposited: 10.0 mJ
Gas mass in arc: 0.02 mg
Temperature rise: 201.8 K
Using constant Cp = 2200 J/(kg·K)

2. Cantera Model (High Fidelity)
------------------------------------------------------------
Energy deposited: 10.0 mJ
Initial temperature: 300.0 K
Temperature rise: 201.8 K
Final temperature: 501.8 K
Cantera not available - using constant Cp fallback

============================================================
Difference: 0.0 K
Models agree well at this temperature range
============================================================

Generating plot: Temperature Rise vs Energy Deposition...

import matplotlib.pyplot as plt
import numpy as np
import openmdao.api as om

from paroto.models.energy_to_temperature import CanteraEnergyModel, ConstantCpEnergyModel

print("=" * 60)
print("Energy to Temperature Conversion Models")
print("=" * 60)

# Example 1: Constant Cp Model (Low Fidelity)
print("\n1. Constant Cp Model (Low Fidelity)")
print("-" * 60)

prob1 = om.Problem()
prob1.model.add_subsystem("e2t", ConstantCpEnergyModel())
prob1.setup()

prob1.set_val("e2t.energy_per_pulse", 10e-3)  # 10 mJ
prob1.set_val("e2t.thermal_diameter", 0.002)  # 2 mm
prob1.set_val("e2t.arc_length", 0.01)  # 10 mm
prob1.set_val("e2t.gas_density", 0.717)  # kg/m³ (CH4)
prob1.set_val("e2t.gas_heat_capacity", 2200.0)  # J/(kg·K)

prob1.run_model()

delta_T1 = prob1.get_val("e2t.delta_T")[0]
m_gas1 = prob1.get_val("e2t.gas_mass")[0]

print("Energy deposited: 10.0 mJ")
print(f"Gas mass in arc: {m_gas1 * 1e6:.2f} mg")
print(f"Temperature rise: {delta_T1:.1f} K")
print("Using constant Cp = 2200 J/(kg·K)")

# Example 2: Cantera Model (High Fidelity)
print("\n2. Cantera Model (High Fidelity)")
print("-" * 60)

prob2 = om.Problem()
prob2.model.add_subsystem("e2t", CanteraEnergyModel())
prob2.setup()

prob2.set_val("e2t.energy_per_pulse", 10e-3)
prob2.set_val("e2t.thermal_diameter", 0.002)
prob2.set_val("e2t.arc_length", 0.01)
prob2.set_val("e2t.gas_density", 0.717)
prob2.set_val("e2t.initial_temperature", 300.0)  # K
prob2.set_val("e2t.pressure", 101325.0)  # Pa

prob2.run_model()

delta_T2 = prob2.get_val("e2t.delta_T")[0]
T_final2 = prob2.get_val("e2t.final_temperature")[0]

print("Energy deposited: 10.0 mJ")
print("Initial temperature: 300.0 K")
print(f"Temperature rise: {delta_T2:.1f} K")
print(f"Final temperature: {T_final2:.1f} K")

try:
    import cantera

    print(f"Using Cantera v{cantera.__version__} with temperature-dependent Cp")
except ImportError:
    print("Cantera not available - using constant Cp fallback")

print("\n" + "=" * 60)
print(f"Difference: {abs(delta_T1 - delta_T2):.1f} K")
if abs(delta_T1 - delta_T2) < 50:
    print("Models agree well at this temperature range")
else:
    print("Significant difference - Cp temperature dependence is important")
print("=" * 60)

# Plot temperature rise vs energy for both models
print("\nGenerating plot: Temperature Rise vs Energy Deposition...")
energy_range = np.linspace(1e-3, 50e-3, 30)  # 1 to 50 mJ
delta_T_const = []
delta_T_cantera = []

for energy in energy_range:
    # Constant Cp model
    prob1.set_val("e2t.energy_per_pulse", energy)
    prob1.run_model()
    delta_T_const.append(prob1.get_val("e2t.delta_T")[0])

    # Cantera model
    prob2.set_val("e2t.energy_per_pulse", energy)
    prob2.run_model()
    delta_T_cantera.append(prob2.get_val("e2t.delta_T")[0])

plt.figure(figsize=(8, 5))
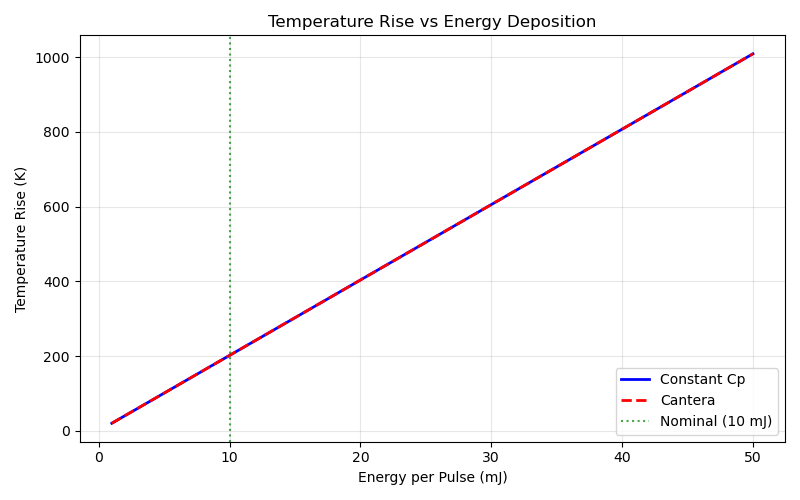
plt.plot(energy_range * 1e3, delta_T_const, "b-", linewidth=2, label="Constant Cp")
plt.plot(energy_range * 1e3, delta_T_cantera, "r--", linewidth=2, label="Cantera")
plt.axvline(x=10, color="g", linestyle=":", alpha=0.7, label="Nominal (10 mJ)")
plt.xlabel("Energy per Pulse (mJ)")
plt.ylabel("Temperature Rise (K)")
plt.title("Temperature Rise vs Energy Deposition")
plt.grid(True, alpha=0.3)
plt.legend()
plt.tight_layout()
plt.show()